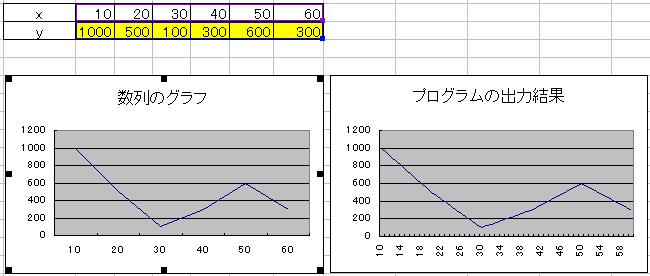
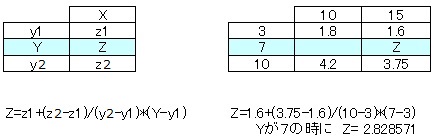
▼2次元でのの線形補間
2次元での線形補間を行うにあたり、1次元のプログラムを修正します。
//線形補間 x:補間する値 ar:数列 w:数列の横の長さ
//offset_x:x軸の左側の距離1次元配列の場合には常に0 offset_y:x軸とy軸との距離、1次元配列の場合には常に1
int interp1dim(const int x,const int*ar,const int w,const int offset_x = 0,const int offset_y = 1){
int i;
//xの値が範囲外の場合はxが最大最小値の値を返す
if(x<=ar[offset_x]){
return ar[(w+offset_x)*(offset_y+1)-w];
}else if(x>=ar[w+offset_x-1]){
return ar[(w+offset_x)*(offset_y+1)-1];
}
for(i=1+offset_x;i<w+offset_x;i++){
if(ar[i]>=x) break;
}
// y=yi + (yi+1-yi)(x-xi)/(xi+1-xi) を行い値を返す
return INTERP(ar[i-1],ar[i],ar[i+(w+offset_x)*offset_y-1],ar[i+(w+offset_x)*offset_y],x);
}
横軸、縦軸にオフセットを入れられるように改造しました。
上記関数を使って2次元で線形補間を行います。
#include <stdio.h>
//線形補間のマクロ
#define INTERP(xi,xi1,yi,yi1,x) (yi + ((( yi1 - yi ) * ( x - xi )) / ( xi1 - xi )))
//数列 最初の-1は数を合わせるためだけです どのような数字でも可能
const int ar[] = {
-1, 10, 20, 30, 40, 50,
10, 110, 120, 130, 140, 150,
20, 210, 220, 230, 240, 250,
30, 310, 320, 330, 340, 350,
40, 410, 420, 430, 440, 450,
50, 510, 520, 530, 540, 550,
60, 610, 620, 630, 640, 650
};
//数列の横の長さ
const int ar_w = 5;
const int ar_h = 6;
//1次元の線形補間 x:補間する値 ar:数列 w:数列の横の長さ
//offset_x:x軸の左側の距離1次元配列の場合には常に0 offset_y:x軸とy軸との距離、1次元配列の場合には常に1
int interp1dim(const int x, const int*ar, const int w, const int offset_x = 0, const int offset_y = 1) {
int i;
//xの値が範囲外の場合はxが最大最小値の値を返す
if (x <= ar[offset_x]) {
return ar[(w + offset_x) * (offset_y + 1) - w];
} else if (x >= ar[w + offset_x - 1]) {
return ar[(w + offset_x) * (offset_y + 1) - 1];
}
for (i = 1 + offset_x; i < w + offset_x; i++) {
if (ar[i] >= x) break;
}
// y=yi + (yi+1-yi)(x-xi)/(xi+1-xi) を行い値を返す
return INTERP(ar[i - 1], ar[i], ar[i + (w + offset_x) * offset_y - 1], ar[i + (w + offset_x) * offset_y], x);
}
//2次元の線形補間 x,y:補間する値 ar:数列 w:数列の横の長さ h:数列の縦の長さ
int interp2dim(const int x, int y, const int*ar, const int w, const int h) {
int i, old = 0;
const int offset_x = 1;
const int offset_y = 1;
const int ar_len = (w + offset_x) * (h + offset_y); //配列の大きさ
const int ar_row = w + offset_x; //配列の一行毎の要素数
for (i = ar_row; i < ar_len; i = i + w + offset_x) {
if (ar[i] >= y) break;
old = i;
}
if (0 == old) {
old = i;
y = ar[i]; //値が範囲から外れていた場合には最小最大値に置換する
} else if (i > ar_len - ar_row) {
i = old;
y = ar[i]; //値が範囲から外れていた場合には最小最大値に置換する
}
//x軸 2軸の値を求める
//i/ar_row old/ar_row にてy軸オフセット値が計算できる
int x1_label = ar[old];
int x1 = interp1dim(x, ar, ar_w, offset_x, old / ar_row);
int x2_label = ar[i];
int x2 = interp1dim(x, ar, ar_w, offset_x, i / ar_row);
if (x1_label == x2_label) { //ラベルが同じだと計算できないため
return x1;
} else {
return INTERP(x1_label, x2_label, x1, x2, y);
}
}
int main() {
int i, j, pos;
printf("\t");
for (i = 5; i <= 65; i += 5) printf("[%d]\t", i);printf("\n");
for (j = 5; j <= 65; j += 5) {
printf("[%d]\t",j);
for (i = 5; i <= 65; i += 5) {
pos = interp2dim(i, j, ar, ar_w, ar_h);
printf("%d\t", pos);
}
printf("\n");
}
return 0;
}
■ VB6での線形補間
ちょっと必要があってVB6で線形補間をするハメになりました。
そこで、元となる配列を定義します。
しかし、VB6では静的な配列は定義できないっぽく要素を一つ一つ代入していくのもクソなので次のようにしました。
ただし、配列はVariantしか使えないし、コードのフォーマットは自動で整えられてしまいクソクソクソです。
数列を作成するためのテスト
Dim ar() As Variant
Private Sub Command1_Click()
Debug.Print UBound(ar)
End Sub
Private Sub Form_Load()
ar = Array( _
1, 2, 3, 4, 5, _
6, 7, 8, 9, 10 _
)
End Sub
出力結果は配列の最大要素数のインデックスである 9 です、要素数ではありません。
ちなみに、 ar(0) には 1 が入り、 ar(9) には 10 が入ります。
以上のC言語との挙動の違いを踏まえて、同様の動作をするようにプログラムを書き直しました。
Option Explicit
Dim ar() As Variant
Dim ar_w As Long
Private Sub Form_Load()
'数列の作成
ar = Array( _
10, 20, 30, 40, 50, 60, _
1000, 500, 100, 300, 600, 300 _
)
'数列の幅を計算
ar_w = (UBound(ar) + 1) / 2
End Sub
'線形補間のマクロ
Private Function INTERP(xi As Long, xi1 As Long, yi As Long, yi1 As Long, x As Long) As Long
INTERP = (yi + (((yi1 - yi) * (x - xi)) / (xi1 - xi)))
End Function
'線形補間 x:補間する値 ar:数列 w:数列の横の長さ
Private Function interp1dim(x As Long, ByRef ar_() As Variant, w As Long) As Long
Dim i As Long
'xの値が範囲外の場合はxが最大最小値の値を返す
If x <= ar_(0) Then
interp1dim = ar_(w)
Exit Function
ElseIf x >= ar_(w - 1) Then
interp1dim = ar_(w * 2 - 1)
Exit Function
End If
For i = 1 To (w - 1) Step 1
If ar_(i) >= x Then Exit For
Next i
' y=yi + (yi+1-yi)(x-xi)/(xi+1-xi) を行い値を返す
interp1dim = INTERP(CLng(ar_(i - 1)), CLng(ar_(i)), CLng(ar_(i + w - 1)), CLng(ar_(i + w)), x)
End Function
Private Sub Command1_Click()
Dim i, j As Long
For i = 10 To 60
j = interp1dim(CLng(i), ar, ar_w)
Debug.Print CStr(i) + vbTab + CStr(j)
Next i
End Sub
値が確認できましたので、時間を使って線形補間をしようと次のようなプログラムを作成しました
Option Explicit
Dim map1() As Variant
Dim map1_w As Long
Private Sub Form_Load()
'数列の作成
map1 = Array( _
0, 1300, 1350, 1400, 1500, 2400, _
100, 100, 500, 1500, 100, 100 _
)
'数列の幅を計算
map1_w = (UBound(map1) + 1) / 2
End Sub
'線形補間のマクロ
Private Function INTERP(xi As Long, xi1 As Long, yi As Long, yi1 As Long, x As Long) As Long
INTERP = (yi + (((yi1 - yi) * (x - xi)) / (xi1 - xi)))
End Function
'線形補間 x:補間する値 ar:数列 w:数列の横の長さ
Private Function interp1dim(x As Long, ByRef ar_() As Variant, w As Long) As Long
Dim i As Long
'xの値が範囲外の場合はxが最大最小値の値を返す
If x <= ar_(0) Then
interp1dim = ar_(w)
Exit Function
ElseIf x >= ar_(w - 1) Then
interp1dim = ar_(w * 2 - 1)
Exit Function
End If
For i = 1 To (w - 1) Step 1
If ar_(i) >= x Then Exit For
Next i
' y=yi + (yi+1-yi)(x-xi)/(xi+1-xi) を行い値を返す
interp1dim = INTERP(CLng(ar_(i - 1)), CLng(ar_(i)), CLng(ar_(i + w - 1)), CLng(ar_(i + w)), x)
End Function
Private Sub Timer1_Timer()
Dim str As String
str = Format(Now, "HH:MM:ss")
Dim m, h, v, pos As Long
m = CLng((CLng(Mid(str, 4, 2)) / 60) * 100)
h = CLng(Mid(str, 1, 2) & "00")
v = h + m
pos = interp1dim(CLng(v), map1, map1_w)
Call logWrite(CStr(pos), "test.txt")
End Sub
Private Sub logWrite(str As String, filename As String)
On Error Resume Next
Dim fileNo As Integer
fileNo = FreeFile
Open App.Path + "\" + filename For Append As #fileNo
Print #fileNo, Format(Now, "yyyy/mm/dd,hh:mm:ss,") + str
Close #fileNo
On Error GoTo 0
End Sub
このプログラムを12時から15時まで走らせれば予想では次のような値を取るはずです。
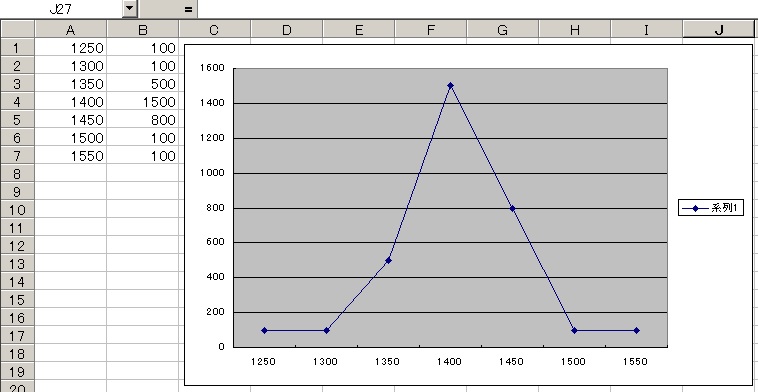
タイマーのインターバルを500msにして動作させて得られた値のグラフが次です。
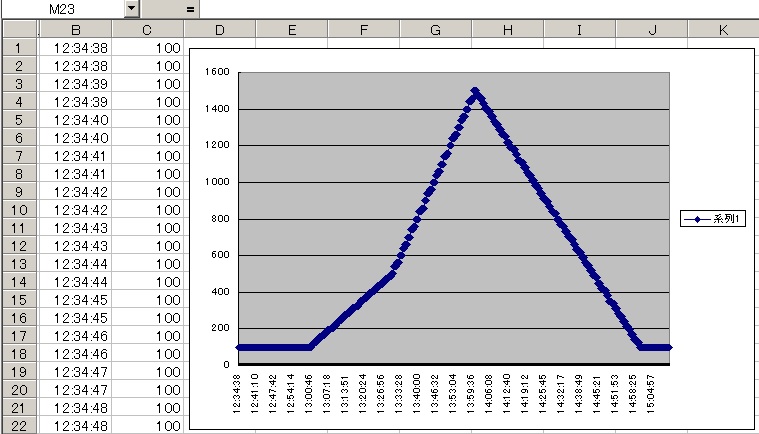
予想と同じ値を取っており、時間による線形補間がうまくいったことを確認できました。
▼ 年初からの経過日数を値として線形補間
年初からの経過日数を値として線形補間をしたいと思います。
そこで、VB6での一年の最初からの日数を返す関数を調べるとします。
日付けの計算はDateDiffで出来るようです。
Debug.Print DateDiff("d", "01/01", Format(Now, "mm/dd"))
戻り値はVariantのLongのようです。
次に、一年の経過日数と月の関連を調べます。
1月1日 年始からの経過日数 0
2月1日 年始からの経過日数 31
3月1日 年始からの経過日数 59
4月1日 年始からの経過日数 90
5月1日 年始からの経過日数 120
6月1日 年始からの経過日数 151
7月1日 年始からの経過日数 181
8月1日 年始からの経過日数 212
9月1日 年始からの経過日数 243
10月1日 年始からの経過日数 273
11月1日 年始からの経過日数 304
12月1日 年始からの経過日数 334
年始からの経過日数 364
DateDiff関数にうるう年の2月29を入力すると前回のうるう年からの日数2223を返しますので注意が必要です。
Debug.Print DateDiff("d", "01/01", "02/29")
ちなみに、2月28日の場合には58が返ります。
365よりも大きな値の場合には58に変更する事でうるう年の問題は解決できそうです。
上記の仕様に従いプログラムを作成しました。
Option Explicit
Dim map1() As Variant
Dim map1_w As Long
Private Sub Form_Load()
'数列の作成
'1月2月 3月 4月 5月 6月 7月 8月 9月 10月 11月 12月
'0, 31, 59, 90, 120, 151, 181, 212, 243, 273, 304, 334,
'1, 10, 20, 30, 50, 80, 100, 300, 200, 10, 100, 150
map1 = Array( _
0, 31, 59, 90, 120, 151, 181, 212, 243, 273, 304, 334, _
1, 10, 20, 30, 50, 80, 100, 300, 200, 10, 100, 150 _
)
'数列の幅を計算
map1_w = (UBound(map1) + 1) / 2
End Sub
'線形補間のマクロ
Private Function INTERP(xi As Long, xi1 As Long, yi As Long, yi1 As Long, x As Long) As Long
INTERP = (yi + (((yi1 - yi) * (x - xi)) / (xi1 - xi)))
End Function
'線形補間 x:補間する値 ar:数列 w:数列の横の長さ
Private Function interp1dim(x As Long, ByRef ar_() As Variant, w As Long) As Long
Dim i As Long
'xの値が範囲外の場合はxが最大最小値の値を返す
If x <= ar_(0) Then
interp1dim = ar_(w)
Exit Function
ElseIf x >= ar_(w - 1) Then
interp1dim = ar_(w * 2 - 1)
Exit Function
End If
For i = 1 To (w - 1) Step 1
If ar_(i) >= x Then Exit For
Next i
' y=yi + (yi+1-yi)(x-xi)/(xi+1-xi) を行い値を返す
interp1dim = INTERP(CLng(ar_(i - 1)), CLng(ar_(i)), CLng(ar_(i + w - 1)), CLng(ar_(i + w)), x)
End Function
Private Sub Timer1_Timer()
Dim str As String
str = Format(Now, "mm/dd")
If str = "02/29" Or str = "2/29" Then str = "02/28"
Dim d, pos As Long
d = DateDiff("d", "01/01", str)
pos = interp1dim(CLng(d), map1, map1_w)
Call logWrite(CStr(pos), "test.txt")
End Sub
Private Sub logWrite(str As String, filename As String)
On Error Resume Next
Dim fileNo As Integer
fileNo = FreeFile
Open App.Path + "\" + filename For Append As #fileNo
Print #fileNo, Format(Now, "yyyy/mm/dd,hh:mm:ss,") + str
Close #fileNo
On Error GoTo 0
End Sub
上記プログラムを走らせたらこのようなグラフが書けるはずです。
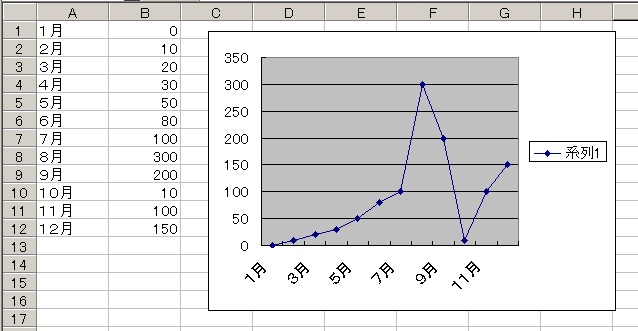
しかし、デバックの為にうるう年の年まで待って1年中プログラムを走らせるわけにもいきません。
最近のうるう年(2月29日)がある年は2020年だそうで、2020年を1月1日から12月31日までぐるっとパソコンの日付の設定を変化させるプログラムを作成するとします。
まずは、パソコン自体の時刻を自動的に設定するをOFFにする必要があります。
2020年1月1日から日付けを加算して変化させるプログラムを作成しました。
標準モジュール
Public i As Integer
フォーム
Private Sub Timer1_Timer()
d = DateAdd("d", i, "2020/01/01")
Date = d
i = i + 1
End Sub
上記プログラムでパソコンの日付を変化させて、デバックの為のデータを出力したグラフです。
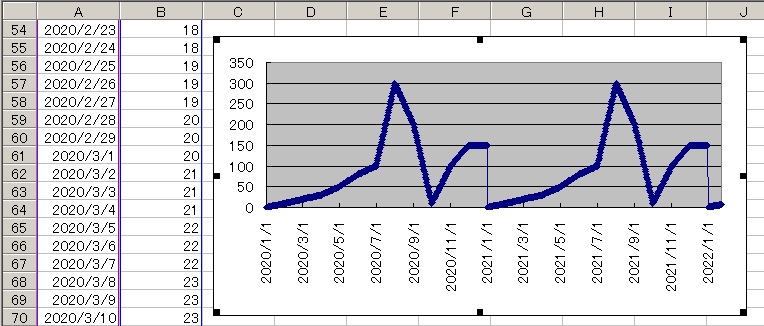
グラフは酷似していて動作は正しいです。
しかし、ふと気が付いたのが12月以降のデータがないため12月は直線のグラフを表しています。
マップに12月以降のデータを追加してみます。
'数列の作成
'1月2月 3月 4月 5月 6月 7月 8月 9月 10月 11月 12月 年末
'0, 31, 59, 90, 120, 151, 181, 212, 243, 273, 304, 334, 366,
'1, 10, 20, 30, 50, 80, 100, 300, 200, 10, 100, 150, 1
map1 = Array( _
0, 31, 59, 90, 120, 151, 181, 212, 243, 273, 304, 334, 366, _
1, 10, 20, 30, 50, 80, 100, 300, 200, 10, 100, 150, 1 _
)
この追加により12月31日の値と1月1日の値が連続するはずです。
これにより作成したグラフが次です。
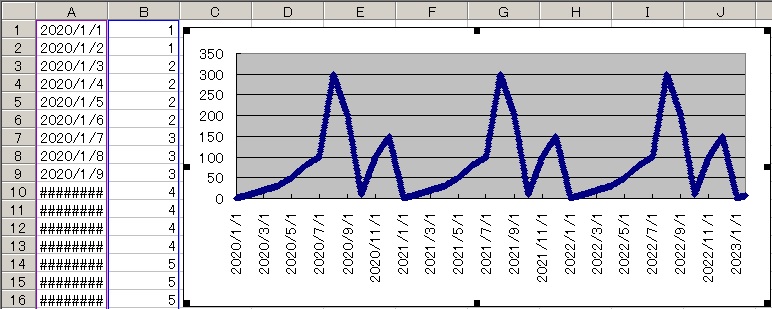
プログラムの動作が正しい事を確認できました。